w El punto: Un punto se representa con una pequeña cruz y se lo designa con una letra de imprenta mayúscula.

w La recta: Una recta se representa con una porción de la misma y se la designa con una letra de imprenta minúscula.

w El plano: Un plano se representa con una porción del mismo y se lo designa con una letra griega.

Relaciones fundamentales
Los tres conceptos anteriores están relacionados a través de las relaciones de pertenencia e inclusión:
w Los puntos pertenecen a las rectas y los planos.

w Las rectas están incluidas en los planos.


Definición
Todo punto perteneciente a una recta separa a la misma en dos porciones, cada una de ellas recibe el nombre de semirrecta. Al punto que da lugar a las dos semirrectas opuestas se lo llama origen.
Para diferenciar las semirrectas se determinan dos puntos adicionales, cada uno de los cuales pertenece a cada semirrecta:
w Semirrecta de origen O que pasa por el punto A
w Semirrecta de origen O que pasa por el punto B


Características de las semirrectas
w Todo punto de una recta pertenece a una de las dos semirrectas o coincide con el origen.
w La intersección de dos semirrectas opuestas es el punto de origen.

w La unión de dos semirrectas opuestas es toda la recta.


Definición
Dados dos puntos A y B, se llama segmento a la intersección de la semirrecta de origen A que contiene al punto B y la semirrecta de origen B que contiene al punto A.
Los puntos A y B se denominan extremos del segmento.

Se observa que:
w Dos puntos pertenecientes a una misma semirrecta determinan un segmento que no contiene al origen.

w Dos puntos pertenecientes a distintas semirrectas determinan un segmento que contiene al origen.

Se verifican las siguientes propiedades:
w Igualdad de segmentos: se verifican las leyes reflexiva, simétrica y transitiva.
w Relación de orden de segmentos: forman un conjunto ordenado.
Igualdad de segmentos
w Carácter reflexivo: todo segmento es igual a si mismo.

w Carácter simétrico: Si un segmento es igual a otro, éste es igual al primero.

w Carácter transitivo: Si un segmento es igual a otro y éste es igual a un tercero, el primer segmento es igual al tercero.

Relación de orden
w Si un segmento es mayor que otro y éste es mayor que un tercero, el primer segmento es mayor que el tercero.

w Si un segmento es mayor que otro y éste es igual a un tercero, el primer segmento es mayor que el tercero.

w Si un segmento es igual a otro y éste es mayor que un tercero, el primer segmento es mayor que el tercero.

Postulado de las tres posibilidades
Dados dos segmentos, debe verificarse una y sólo una de las siguientes tres posibilidades:

http://www.escolar.com/avanzado/geometria001.htm

Definición
Cuando dos rectas se cortan, forman en el plano 4 regiones llamadas ángulos.
Dados dos planos se llama ángulo convexo 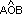 a la intersección del semiplano respecto de la recta
a la intersección del semiplano respecto de la recta 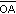 que contiene al punto B y el semiplano respecto a la recta
que contiene al punto B y el semiplano respecto a la recta 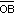 que contiene al punto A.
que contiene al punto A.
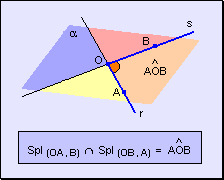
Si en cambio, se considera la unión de los dos semiplanos queda determinado un ángulo cóncavo. Si se suprime un ángulo convexo del plano, lo que queda es un ángulo cóncavo.
Las relaciones angulares verifican las siguientes propiedades:
w Igualdad de ángulos: se verifican las leyes reflexiva, simétrica y transitiva.
w Relación de orden de ángulos: forman un conjunto ordenado.

Identificación de un ángulo
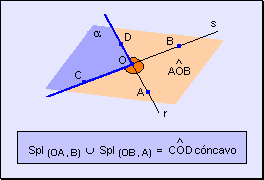
Por lo tanto, un ángulo es la porción de plano delimitado por dos semirrectas del mismo origen, y está delimitado por:
w Un vértice: punto de origen de las dos semirrectas que lo forman.
w Dos lados: semirrectas cuyo origen forma el vértice del ángulo.
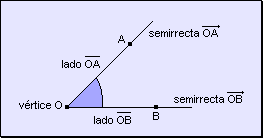
Los ángulos se identifican por tres letras donde:
· La letra central corresponde al vértice.
· Las otras dos letras son puntos cualesquiera de las semirrectas que lo forman.
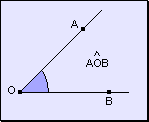
Cuando los lados del ángulo son dos semirrectas opuestas se denomina ángulo llano. El ángulo llano a un semiplano.


Punto interior a un ángulo
Todo punto perteneciente a un ángulo que no pertenece a sus lados se llama punto interior al ángulo.
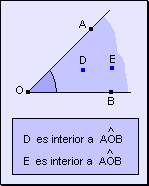
Semirrecta interior a un ángulo
Toda semirrecta cuyo origen coincide con el vértice del ángulo y sus demás puntos son interiores al ángulo se llama semirrecta interior al ángulo.
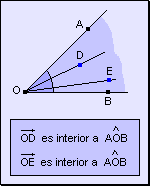
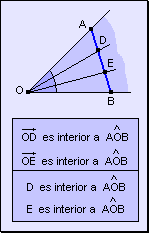
Segmento y ángulo
Si un segmento tiene sus extremos en los lados de un ángulo, toda semirrecta interior a ese ángulo corta al segmento en un punto interior al ángulo.
Plano:
Es uno de los entes geométricos fundamentales, junto a la recta y el punto. Son considerados conceptos primitivos, o sea que no es posible definirlos con base a otros elementos ya conocidos. Sin embargo es posible elaborar definiciones de ellos, con base a los Postulados característicos, que determinan relaciones entre los entes fundamentales.
es.wikipedia.org/wiki/Plano

Definición
Toda recta perteneciente a un plano separa al mismo en dos porciones, cada uno de ellos recibe el nombre de semiplano. A la recta que da lugar a los dos semiplanos se la llama frontera o recta de división.
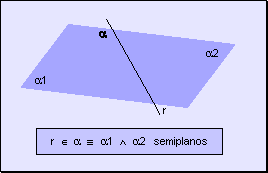
Para diferenciar los semiplanos se determinan dos puntos adicionales, cada uno de los cuales pertenece a cada semiplano:
w Semiplano respecto a la recta r que contiene al punto A
w Semiplano respecto a la recta r que contiene al punto B
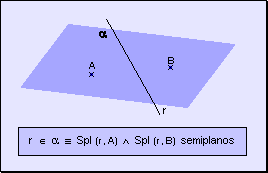

Propiedades de los semiplanos
Se observa que:
w La intersección de dos semiplanos determinados por una recta es la recta de división.
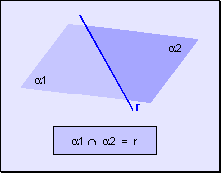
w La unión de dos semiplanos determinados por una recta es todo el plano.
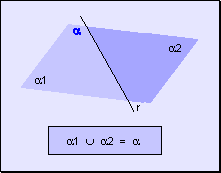
w Todo punto de un plano pertenece a uno de los dos semiplanos o a la recta de división.
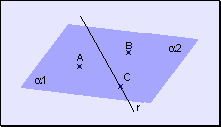
w Todo segmento determinado por dos puntos de distintos semiplanos corta a la recta de división.
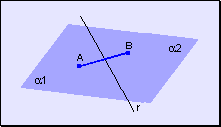
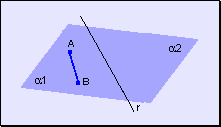
w Todo segmento determinado por dos puntos del mismo semiplano no corta a la recta de división.
http://www.escolar.com/avanzado/geometria005.htm
RAYO:
rayo - Un rayo es una parte de una línea que tiene un punto extremo y se extiende infinitamente en una dirección.
http://www.mathnotes.com/aw_span_gloss.html#anchor82384
3. Explicar el porqué el punto, la recta y el plano no pueden ser definidos.
4. Asociar las ideas de punto, recta y plano a objetos del aula.
Punto:
El clavo de la mesa.
El punto del cpu para reniciar la maquina. Imágenes relacionadas con los restos arqueológicos de Moche- Chimú, así como también con objetos y lugares del aula.
El punto del plumon en la pizarra, etc.
Recta:
El borde de la mesa y de la pizarra.
El borde del muro.
El borde del cuadro.
Las rayas en las paredes de Chan Chan, etc.
Plano:
El piso del aula.
La mesa.
Las paredes.
Las paredes de Chan Chan, etc
6. Construir y medir de ángulos, utilizando el transportador.


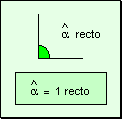
7. Mostrar ejemplos de ángulos de , 90 grados , 180 grados; y 360 grados.
9. angulos formados por 2 rectas paralelas cortadas por una secante.
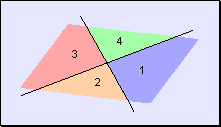
Si intersectamos dos rectas con una secante, se forman de manera natural ocho ángulos, cuatro en cada punto de intersección.
En el caso de rectas paralelas cortadas por una secante, se verifica que los ángulos correspondientes son de igual medida, al igual que los ángulos alternos internos y alternos externos. En resumen, para el caso de rectas paralelas cortadas por una secante los ángulos 1-3-5-7 son iguales entre si, del mismo modo que los ángulos 2-4-6-8.
10. Problemas de angulos.
1.









































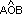 a la intersección del semiplano respecto de la recta
a la intersección del semiplano respecto de la recta 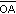 que contiene al punto B y el semiplano respecto a la recta
que contiene al punto B y el semiplano respecto a la recta 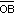 que contiene al punto A.
que contiene al punto A.